You are to inflict maximum damage to the zerg army. There are two types of units - Warrior and Shield. Warriors do damage every second, while a shield protects your entire army for one second. Your army is instantly overrun after the shield generators expire. Given \(G\) cost to build a shield, \(W\) cost to build a warrior and total money \(M\), how many shields would you build?
Solution
Let \(X\) and \(Y\) be the optimal number of generators and number of warriors to be built, respectively. Let’s start with a simple concrete example. Suppose shields and warriors both cost 1 unit and you have total money of 5 units. Also assume 1 unit of damage per warrior. What is the optimum value of \(X\) and \(Y\)? It would be optimum if you can inflict maximum damage. With 5 units of money, you can buy shields/warriors in the following combinations.
| X | Y | Damage |
|---|---|---|
1 |
4 |
4 |
2 |
3 |
6 |
3 |
2 |
6 |
4 |
1 |
4 |
In this case, the optimal choice of \(X, Y\) seem to be \((2, 3)\) and \((3, 4)\) respectively, both of which maximize the product \(XY\). In the general case, the cost to buy \(X\) generators is \(XG\), cost to buy \(Y\) warriors is \(YW\). Since we are limited by \(M\) amount of money, \(X, Y\) must satisfy \(XG + YW \le M\). This can be represented as a line and the inequality encapsulates a region for candidate \((X, Y)\) values.
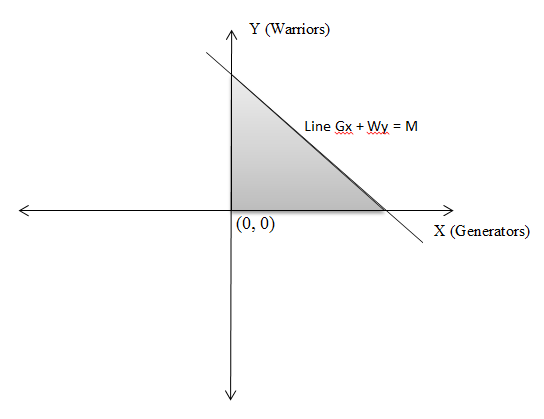
We want \(X, Y \mid \arg\max{XY} \). Geometrically, \(XY\) represents the area of the rectangle shaded in blue.
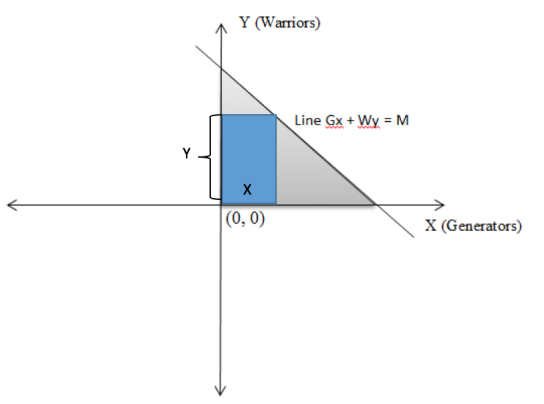
We need to find integer values of \(X, Y\) that maximize this area.
How do we go about doing that? We know that the line will intersect X and Y axis at \(\frac{M}{G}, \frac{M}{W}\). We also know that the optimal rectangle touches the line. If it doesn’t, the area can be trivially increased by increasing either/both \(X, Y\) values until it touches the line.
The boring calculus way for figuring this out is as follows:
\(Area(A) = XY \\ A = \frac{M - YW}{G}Y \\ \\ \frac{\partial A}{\partial Y} = \frac{Y(M - WY)}{G} \\ \arg\max{A} \scriptstyle \implies \frac{Y(M - WY)}{G} = 0 \\ Y = \frac{M}{2W} \)
This gives corresponding \(X = \frac{M}{2G}\)
A more interesting way to arrive at the same conclusion would be to think as follows:
-
The shaded triangle increases its area as long as X and Y increase.
-
Start with \((0, 0)\) and increase both \(X, Y\) by 1. This gives us a small rectangle with bottom left \((0, 0)\) and top right \((1, 1)\).
-
If the straight line was X + Y = 1, it would be a right angled isosceles triangle. The \(X, Y\) value would always increase in the direction of line \(Y = X\), which would cut the line in middle at \((\frac{X}{2}, \frac{Y}{2})\)
-
Generalizing this, the value of \(X. Y\) will increase as long as we go on the direction of line that joins \((0, 0)\) to midpoint of the line \(XG + YW = M\). The mid point of this line is, unsurprisingly, \((\frac{M}{2G}, \frac{M}{2W})\)
There are other ways to arrive at this. Perhaps I should write a post that exclusively deals with this problem.
Coming back to our original question, the optimal number of shields must be \(\frac{M}{2G}\). If, \(\frac{M}{2G}\) is not an integer, we go towards the origin on the line that joins \((0, 0)\) and \((\frac{M}{2G}, \frac{M}{2W})\). However, I was able to get away by taking \(\lfloor\frac{M}{2G} \rfloor\).