Typically, a genetic algorithm works by the notion of maximizing the fitness. Consider a function \(y = x\), which is to be minimized in the interval \([-5, 5]\). One approach is use \(\frac{1}{x}\) as the fitness function. Intuitively, by maximizing \(\frac{1}{x}\), we are minimizing \(y = x\). However, a plot of \(\frac{1}{x}\) reveals some serious flaws.
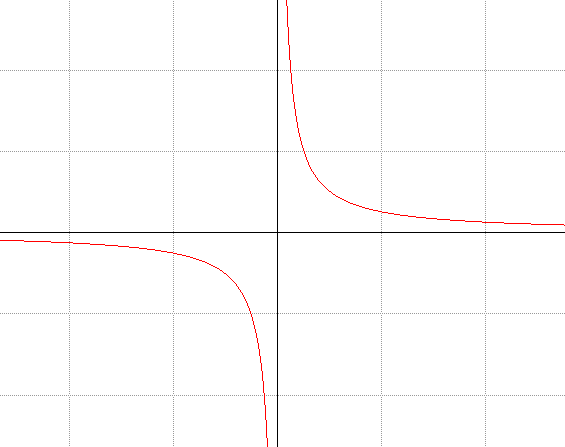
If we move from the right, the maximum occurs at \(x = 0\) instead of \(x = -5\). Why? because \(\frac{1}{x}\) is not differentiable at \(x = 0\). Always make sure that the fitness/loss function is differentiable! In this case, it is better to use \(y = -x\) as the fitness function.
In general, if we are seeking to minimize \(y = f(x)\), where \(f(x)\) is differentiable, then it is safer to use \(y = -f(x)\) as the fitness function. Probably very obvious, but I got burned by this.