Facebook hacker cup: Geometric approach to double squares problem

Given an integer \(N\), we need to find the number of integral pairs \((x, y) \mid x^2 + y^2 = N\), \(N \in [0, 2147483647]\), with a maximum of 100 such numbers in a file.

Solution

Geometrically, we know that \(x^2 + y^2 = r\) represents a circle centered at \((0,0)\) with a radius \(r\). So, the problem can be interpreted visually as finding all possible solutions where \(x, y\) are positive, i.e., lie in the first quadrant.

Testing all possible integral pairs of \((x, y)\) upto \(N\) is equivalent to searching within the grayed geometric square as illustrated.

Figure 1. Geometric view of double squares problem

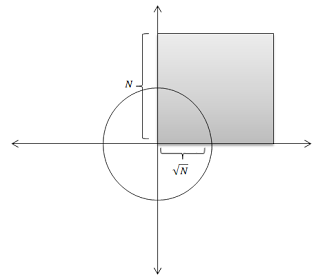
Algorithmically, this approach takes \(O(n^2)\) time. Consider the sample input as shown below (this was the file I received)

On my machine, brute force approach takes approx 14 minutes (!!!) to solve this input. Clearly, we are exploring a lot of unwanted points. One obvious way to improve this is to explore points bounded by the circle as as indicated by the shaded blue square.

Figure 2. Improving on naive search

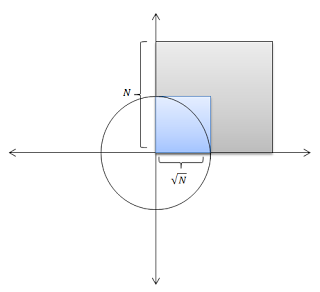
This makes intuitive sense since \(x, y\) cannot exceed \(\sqrt{n}\). This reduces the complexity from \(O(n^2)\) to \(O(n)\) reducing execution time from an earlier 14 minutes to 80.5 secs.

Can we do any better? Why explore the entire blue square? It is sufficient if we examine all points on the arc of the circle in the first quadrant. i.e, increment \(x\) from \([0, \sqrt{n}]\), compute corresponding \(y = \sqrt{n - x^2}\) and check if it is an integer. \(y\) is an integer if \(\lfloor y \rfloor == y\).

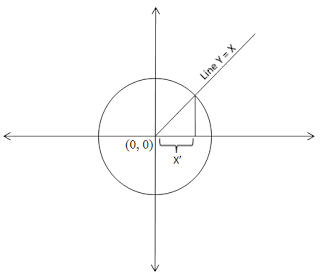
This looks pretty good. Is there anything else that can be improved upon? Well, if you notice the figure carefully, we don’t have to iterate \(x\) from \([0, \sqrt{n}]\). All points on one side of line \(y = x\) are mirror images of points on the other side. i.e., if we find a point, day \((3, 4)\) then we will find a mirror \((4, 3)\) on the other side. Since the problem doesn’t differentiate between these two solutions, it is sufficient if we iterate \(x\) from \([0, x']\), where \(x'\) is given by \(\sqrt{n} \cos{45} = \sqrt{n/2}\).

Figure 3. Line \(y = x\) acts as a mirror

With this, we can complete the algorithm in java as follows:

int getNumSumSquares(final int n)
{
	if(n == 0) {
		return 1;
    }

	final int iterations = (int) Math.ceil(Math.sqrt((n * 1.0)/2)) + 1;
	double y;
	int count = 0;
	for(int x = 0; x <= iterations; x++)
	{
		y = Math.sqrt(n - (x*x));
		// check if y is an integer
		if (Math.floor(y) == y) {
			count++;
        }
	}
	return count;
}

This algorithm works in \(O(\sqrt{n/2}) \sim O(\sqrt{n})\). This only takes 0.047 secs to execute!